Compact Sets are Closed and Bounded - YouTube
Examples of Open, Closed, Bounded and Unbounded Sets - YouTube
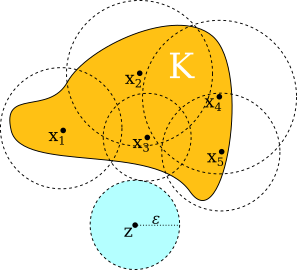
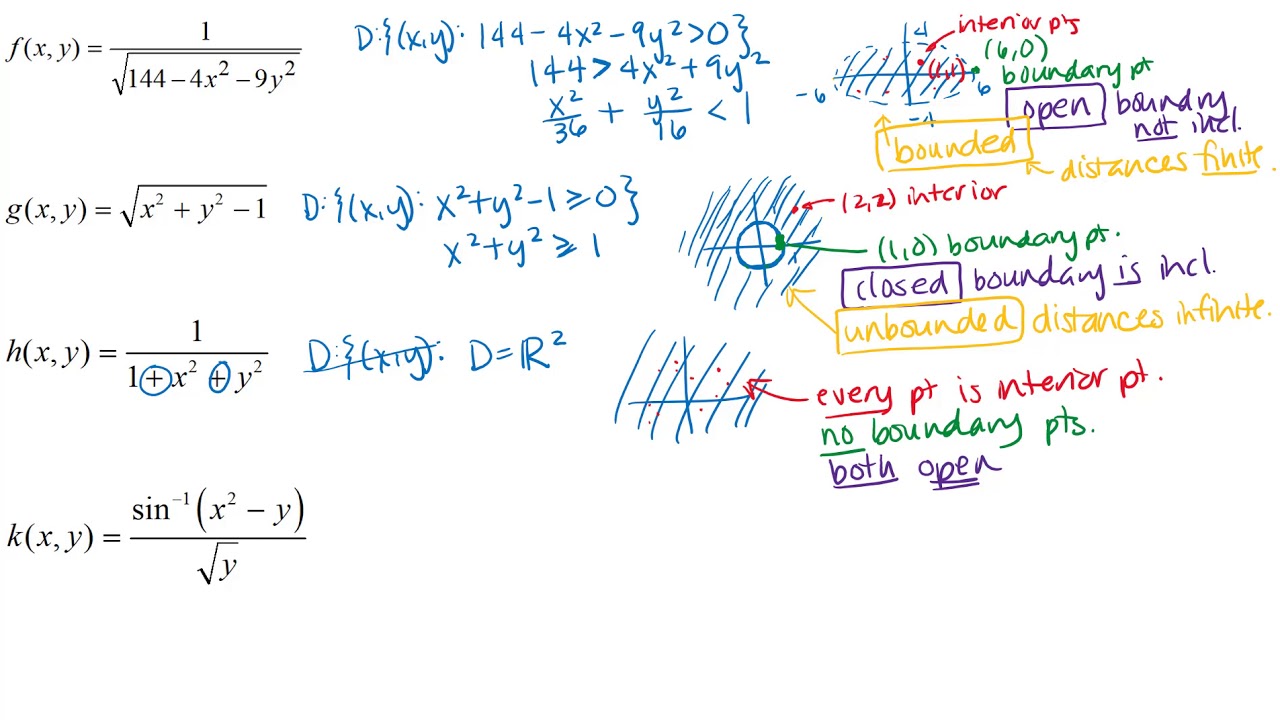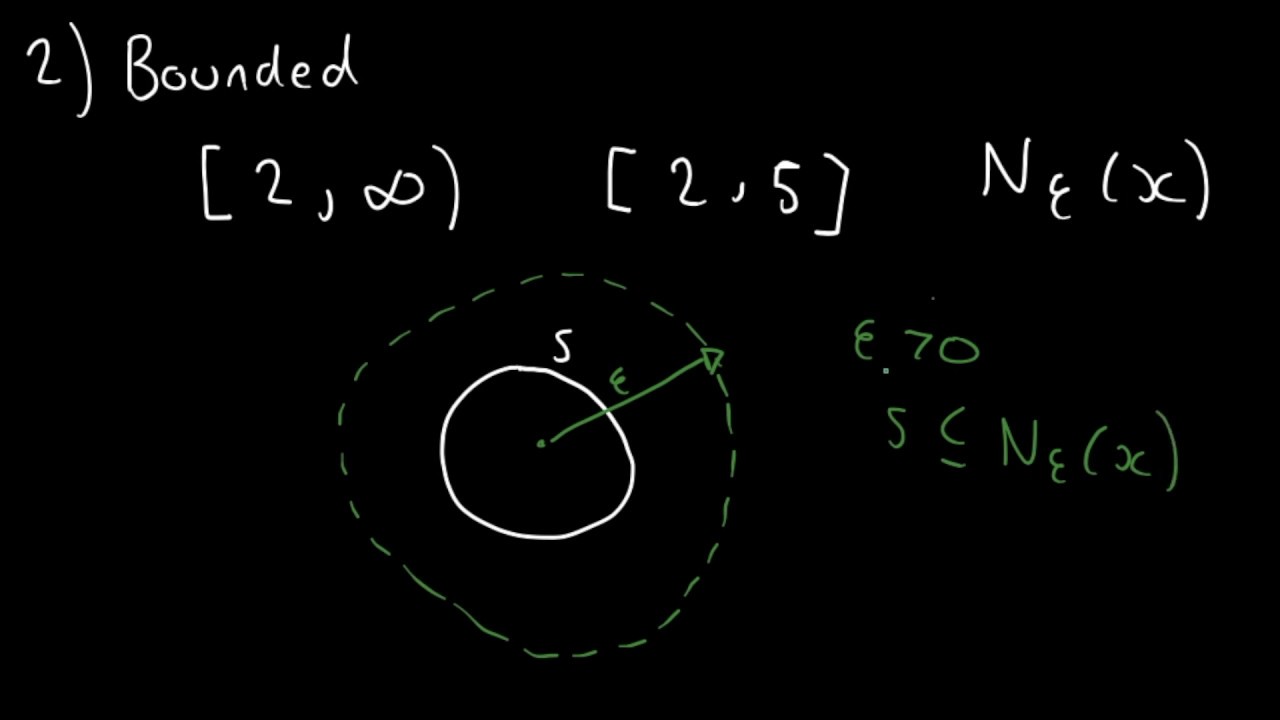SOLVED: Exercise 1.4.1. A set A of a metric space is said to be bounded if it is contained in some ball B(x, r). Show that a subset of a metric space
Metric Spaces: Compactness
mathsub.com on X: "Compact sets can be tough to imagine, but in Euclidean space, the Heine-Borel Theorem helps a lot! #MathGRE #Analysis https://t.co/enMHYJYfyt" / X
Understanding Compact Sets - YouTube
Compactness with open and closed intervals - YouTube
Topology: More on Compact Spaces | Mathematics and Such
![SOLVED: Compactness Chapter 3-6: Connectedness 5 172 subset of R is compact in the topology Jf. (See Show that every Example € of R in the topology 6, Is [0, 1] compact](https://cdn.numerade.com/ask_images/a93ccef562ef4db9a507dffa74b4fc12.jpg "SOLVED: Compactness Chapter 3-6: Connectedness 5 172 subset of R is compact in the topology Jf. (See Show that every Example € of R in the topology 6, Is [0, 1] compact")
SOLVED: Compactness Chapter 3-6: Connectedness 5 172 subset of R is compact in the topology Jf. (See Show that every Example € of R in the topology 6, Is [0, 1] compact
Closedness of Compact Sets in a Metric Space - Mathonline
The Extreme Value Theorem for Cts. Fns. on Comp. Sets of Met. Sps. - Mathonline
Compact Sets are Closed and Bounded - YouTube
Topology: Sequentially Compact Spaces and Compact Spaces | Mathematics and Such
Solved Problem 5 (Fancy example of a closed and bounded set | Chegg.com
Compact Set, Proper Spaces and Annulus - Cheenta
Analysis WebNotes: Chapter 06, Class 31
Answered: Let (X, d) be a metric space. In this… | bartleby
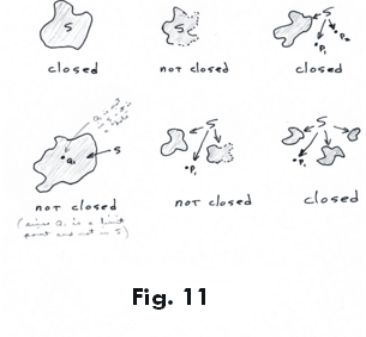
Point sets in one, two, three and n-dimensional Euclidean spaces. Neighborhoods, closed sets, open sets, limit points, isolated points. Interior, exterior and boundary points. Derived set. Closure of a set. Perfect set.
Open Set, Closed Set, Bounded Set, Compact Set, Connected Set: Topology part-3 - YouTube
Solved 11. (i) Prove that every finite subset of R" is | Chegg.com
general topology - Determining if following sets are closed, open, or compact - Mathematics Stack Exchange
Continuous Functions on Compact Sets of Metric Spaces - Mathonline
calculus - What is the difference between "closed " and "bounded" in terms of domains? - Mathematics Stack Exchange
Let $A$ be a closed and bounded subset of $\mathbb{R}$ with the standard (order) topology. Then $A$ is a compact subset of $\mathbb{R}$. - Mathematics Stack Exchange
